Blog

Binary Search Trees: The concept of Binary Search Trees (BSTs), is one of the most fundamental data structures in computer science. This article will discuss the properties, operations, advantages, and real-world applications of Binary Search Tree.

What is a Binary Search Tree?

A Binary Search Tree (BST) is a hierarchical data structure that organizes data to allow for fast search, insertion, and deletion operations. A BST ensures that the values in its nodes are arranged in a specific order to optimize lookup time, making it ideal for tasks that involve frequent data retrieval.

Properties of a Binary Search Tree

The Binary Search Tree has a specific set of rules that dictate how data is organized:

1. Node Structure: Each node in the BST contains:
   • Data: The actual value stored.
   • Left Child: A pointer/reference to the left subtree.
   • Right Child: A pointer/reference to the right subtree.
2. Ordering Rule:
   • The value in the left subtree of a node is always smaller than the node itself.
   • The value in the right subtree of a node is always larger than the node itself.
   • Both subtrees must also follow the same properties, ensuring that the entire structure adheres to the BST ordering rules.

Operations on a Binary Search Tree

The true power of a BST lies in its ability to handle various operations efficiently. Let’s take a look at the primary operations:

1. Search Operation:
   • Start from the root node and compare the target value with the node’s value.
   • If the value matches, the search is successful.
   • If the target value is smaller, move to the left subtree.
   • If the target value is larger, move to the right subtree.
   • Repeat this process until the value is found or the subtree is empty.
   Time Complexity:
   • Average case: O(log⁡n)
   • Worst case: O(n) when the tree is skewed.
2. Insertion Operation:
   • Start at the root and traverse down the tree.
   • If the value is smaller than the current node, move to the left subtree; if larger, move to the right.
   • Insert the value when you reach an empty position.
   Time Complexity:
   • Average case: O(log⁡n)
   • Worst case: O(n)
3. Deletion Operation: Deleting a node from a BST requires special handling:
   • Case 1: The node is a leaf (has no children). In this case, simply remove the node.
   • Case 2: The node has one child. Replace the node with its child.
   • Case 3: The node has two children. Replace the node with its in-order successor (smallest node in the right subtree) or in-order predecessor (largest node in the left subtree), then delete the successor or predecessor.
   Time Complexity:
   • Average case: O(log⁡n)
   • Worst case: O(n)

Read also: Abstract Class in Java: A Comprehensive Overview with 5 Examples

Why is Tree Balancing Important?

One potential drawback of a BST is that if elements are inserted in a sorted order, the tree can become skewed, leading to performance degradation. In such cases, the tree resembles a linked list, with time complexity O(n)O(n)O(n) for operations.

To address this, self-balancing trees like AVL Trees and Red-Black Trees were introduced, ensuring that the height of the tree remains balanced. These trees automatically adjust themselves during insertions and deletions to maintain efficient search times.

Advantages of Using a Binary Search Tree

The BST offers several advantages that make it a widely-used data structure:

• Efficient Searching: With a time complexity of O(log⁡n) on average, BSTs allow for quick lookups, especially when compared to unsorted data structures.
• Sorted Data: An in-order traversal of a BST results in data sorted in ascending order, providing easy access to sorted data without additional sorting steps.
• Dynamic Structure: Unlike static arrays, BSTs allow for dynamic insertion and deletion, providing flexibility when working with changing data sets.

Read also: Java program for Stack

Real-World Applications of Binary Search Trees

BSTs are incredibly useful in a wide range of real-world applications, including:

• Database Management: Indexing data for faster lookup in databases, allowing quick searches for records.
• Search Engines: Storing keywords or phrases to efficiently retrieve relevant documents.
• Network Routing Algorithms: Determining optimal routing paths by quickly searching network nodes.
• Symbol Tables in Compilers: Storing variables and function identifiers for efficient symbol resolution during compilation.

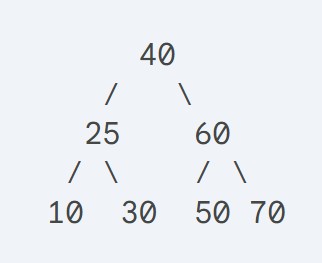
Example: Constructing a Binary Search Tree

Let’s consider an example where we insert the following values into a BST in this order: 40, 25, 60, 10, 30, 50, 70.